Due to the unique crystal shape, tuning fork crystals do not provide high accuracy over a wide temperature range. Their temperature accuracy can be plotted as a parabolic curve over temperature. This accuracy is typically ±20ppm at room temperature or roughly +25°C. This is the equivalent of gaining or losing 1.728seconds of time each day or 10.512 minutes per year. The figure below shows the decrease of accuracy at extreme high and extreme low temperatures.

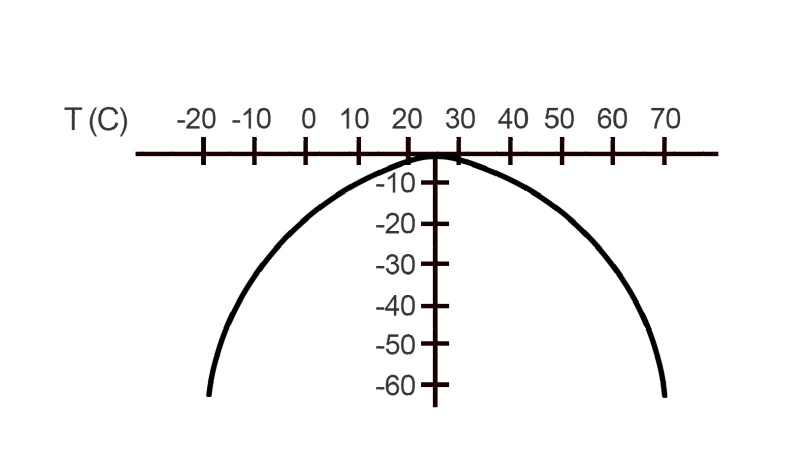
Parabolic curve to determine tuning fork frequency stability

How to Determine the Temperature versus Accuracy of a Typical 32.768 kHz Tuning Fork Crystal

The frequency deviation (Δf) of a typical crystal at a specific frequency (f) and temperature (T) is:

Δf/f = k(T – T_o)² + f_o

Where:

• f is the nominal crystal frequency
• k is the curvature constant
• T is the temperature
• T_o is the turnover temperature
• f_ois the frequency deviation at room temperature

An analysis of this equations reveals only three variables that control a crystal’s frequency response over temperature. These are the curvature contact, turnover temperature, and room temperature frequency deviation. The curvature constant has the most effect on the parabolic nature of the frequency deviation over temperature, but this constant has a very small deviation. Different turnover temperatures shift the deviation curve left or right and different frequency deviations at room temperature will shift the curve up or down.